As
we all are aware of how important mechanics is in physics, here are more tips
to solve problems further. Though intensive practice is required in mechanics ,
it is essential to know how to solve the problems too….
Here
are few ways to approach problems in mechanics…
In
a PLANE :
In
such type of problems, do follow the below:
i. The
very first step required is to select a coordinate system and resolve the velocity
vector into its individual x and y components.
ii. Next,
find out the respective acceleration in each direction and solve according to the
equation of rectilinear motion.
iii. Now,
if you find acceleration only in vertical direction, follow the methods for
solving constant-acceleration problems to analyze the vertical motion. The
motion in x and y have the same time of flight t.
iv. If
there is any problem relating to the trajectory, find the motions in x and y
direction with respect to time from the previous point and from one equation,
find the value of t and substitute that in another equation to find out the
equation of the trajectory.
i. To
solve such problems, just select one coordinate system and resolve the velocity
into x, y and z directions.
ii. The
acceleration in each direction can be found out and solved according to the
equation of rectilinear motion.
i. To
approach any problem, the very first thing needed to be done is to draw a
neat diagram of the system.
ii. Next,
consider all the forces and their origin on each object. Find out the forces
acting on each object. Note down all the contact forces wherever there is a
contact.
iii. Calculate
the centripetal force required for the motion which is circular.
The
velocity can be found accordingly with the centripetal force = mv2/R.

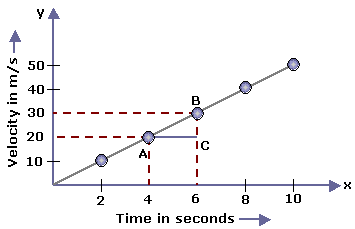







 .
.




 .
.

 .
.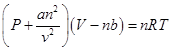
 .
.




 .
. ,
,  is
is 
 is called a
homogenous equation of degree 2
is called a
homogenous equation of degree 2 
 ,lines are
coincident.
,lines are
coincident.


 ,
,  .
. is
is  .
. .
.
 .
.





 to represent a
pair of straight lines is that
to represent a
pair of straight lines is that
 .
. are given by
are given by  .
.

 .
.

 and a straight
line
and a straight
line  is
is 
 =0 and
=0 and  is
is 